Minimum Edit Distance.
1. Minimum Edit Distance
When you use some text editors like MS Word, you’ll find there is a function called “spell correction”, it will give a list of words that it think you might want to replace with. How comes this list? Here we’d like to introduce a basic concept in NLP called Minimum Edit Distance.
Minimum Edit Distance is the minimum number of editing operations (insertion, deletion, substitution) that needed to transform one text to another. This is also known as Levenshtein distance.
Now you may have a idea how spell correction function works, it should give the words that have the minimum edit distance to the word you just typed in! (we assume you have a typo) Besides spell correction, minimum edit distance also can be applied in following cases:
- inference alignment in computational biology: DNA sequences
- evaluate machine translation and speech recognition
- named entity extraction and entity coreference
2. Find Minimum Edit Distance
To deal with this, you’d better think algorithmically: we are actually searching for a path from start string to final string. We have 4 elements:
- initial state
- operators (insert, delete, substitute)
- goal state
- path cost
The space of all path is huge, if you have algorithm basis you must know that brute force searching is expensive that we will never use, and there are many paths will end up with the same results. We don’t need to keep track of all of them, we just need to find a shortest path.
3. Formulation
Assume we have two texts: \(x\) with length \(n\) and \(y\) with length \(m\), define \(d(i, j)\) to be the edit distance between \(x[1:i]\) and \(y[1:j]\), therefore the edit distance between \(x\) and \(y\) is \(d(n, m)\).
You can see there are two parameters for the edit distance, we can demonstrate it on tabular and this is same as Dynamic Programming Don’t worry if you don’t know that, dynamic programming is a way to solve problems by combining solutions to subporblems, it’s a “bottom-up” method.
Apply to this case, we compute \(d(i, j)\) for small \(i, j\) and then compute larger \(d(i, j)\) based on previously results, step by step. For dynamic problem, we need to write the recurrence form:
\[
d(i, j) = \min\left\{
\begin{aligned}
&d(i-1, j)+1,\\
&d(i, j-1)+1,\\
&d(i-1, j-1)+\left\{
\begin{aligned}
&2, \text{ if } x[i] \neq y[j]\\
&0, \text{ if } x[i]=y[j]
\end{aligned}
\right.,
\end{aligned}
\right..
\]
where \(d(i,0)=i\) and \(d(0,j)=j\), the algorithm will terminate when \(i=n\) and \(j=m\).
Next is an example, we’d like to calculate the edit distance between “intention” and “execution”, the initial table is this
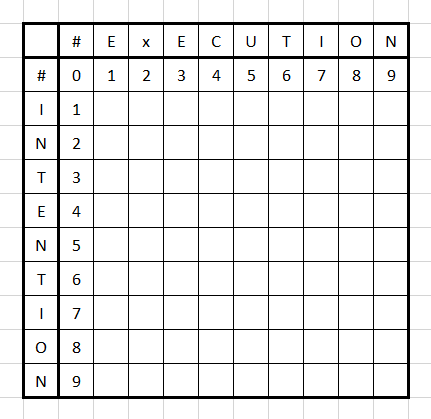
Now based our formula, we can calculate that
\[
d(1, 1) = \min\left\{
\begin{aligned}
&d(0, 1)+1\\
&d(1, 0)+1\\
&d(0, 0)+2
\end{aligned}
\right. = \min\{2, 2, 2\} = 2,
\]
\[
d(2, 1) = \min\left\{
\begin{aligned}
&d(1, 1)+1\\
&d(2, 0)+1\\
&d(1, 0)+2
\end{aligned}
\right. = \min\{3, 3, 3\} = 3.
\]
And finally we can get the following plot, the red numbers consist the all of the edit distance for \(i=1\) to \(9\) and for \(j=1\) to \(9\).
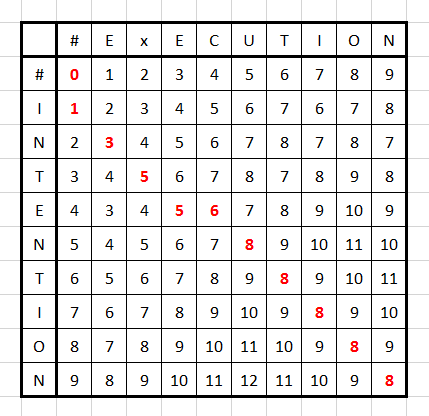
4. Backtrace for Computing Alignment
Sometimes edit distance isn’t sufficient, we often need to align each character of the two strings to each other (the example we use above are equal length). Which means we need to remember where we came from when we enter a new cell in above tabular.
In summary, the time complexity for finding minimum edit distance is \(O(nm)\), space complexity is \(O(nm)\), and for backtrace it is \(O(n+m)\).
5. Weighted Edit Distance
We can also add some weight (cost) to each kind of operation and use the sum of the cost as the minimum edit distance. For example, in spell correction, some letters have higher probability to be mistyped.