[Paper reading] A Neural Probabilistic Language Model.
1. Introduction
Language model (Probabilistic) is model that measure the probabilities of given sentences, the basic concepts are already in my previous note Stanford NLP (coursera) Notes (4) - Language Model. This paper by Yoshua Bengio et al uses a Neural Network as language model, basically it is predict next word given previous words, maximize log-likelihood on training data as Ngram model does.
Another important thing to notice - distributed word feature vector is learned simultaneously, as you all know Word Embeddings.
2. Highlights
The idea comes from “fighting with Curse of Dimenstionality” - For classical language model, e.g. the vocabulary size is 100000, train on a sentence with 10 words will get potentially \(100000^{10} - 1\) parameters - because the test sentence is unseen.
2.1 Introduction
The idea of improvement is summarized as follows:
- associate with each word in vocabulary a distributed word feature vector
- express the joint probability function of word sequences in terms of feature vectors of these words in sentence
- learn simultaneously the word feature vectors and parameters of the probability function
Advantage: generalization is obtained because a sequence of words that has never seen before gets higher probability if it’s made of words that are similar to words forming an already seen sentence - where in ngram model, word similarity between words are not take into account.
2.2 Relation to Previous Work
Using neural networks to model high-dimensional discrete distribution is not first introduced here, it already been found. The model presented here could extend to large scale data.
The idea of using word similarity is also not new, same for vector-space representation for words. Here the paper use word vectors to measure simiarlitiy between words.
2.3 Model
- Training data: \(w_{1}, w_{2},\cdots, w_{T}\) where \(w_{t}\in V\)
- Objective: learn probability function (conditional probability):
\[
f(w_{t},w_{t-1}\cdots,w_{t-n+1}) = P(w_{t}|w_{1},\cdots,w_{t-1})
\]
where \(\sum^{|V|}_{w_{t}} f(w_{t},w_{t-1},\cdots,w_{t-n+1}) = 1\).
Decompose \(f(w_{t},w_{t-1}\cdots,w_{t-n+1})\) in 2 parts:
- A mapping \(C\) from word (index \(i\)) in \(V\) to a real vector \(C(i)\in\mathbb{R}^{m}\). Overall \(C\) is represented by a lookup matrix with size \(|V|\times m\)
- A probability function over words expressed with \(C\) - function \(g\) maps inpute sequence of word feature vectors for words in context \(\left[C(w_{t-n+1})\cdots C(w_{t-1})\right]\), to a conditional probability distribution over words in \(V\) for next \(w_{t}\). The output of \(g\) is a vector whose \(i\)-th element is the estimate of \(P(w_{t}|w_{1},\cdots,w_{t-1})\).
In summary,
\[
f(w_{t},w_{t-1}\cdots,w_{t-n+1}) = g(i, C(w_{t-n+1})\cdots C(w_{t-1})).
\]
The model (neural network) structure in paper:
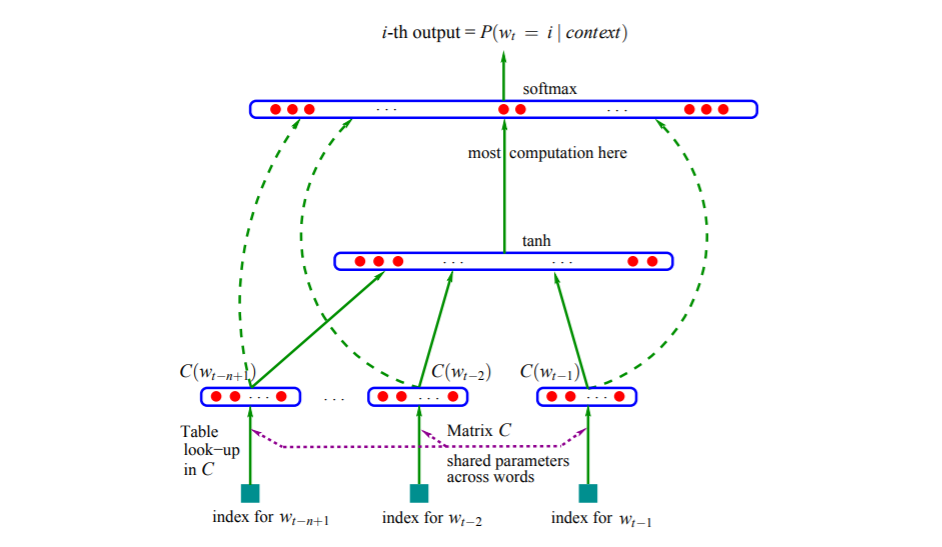
As \(C\) is shared across all words in context. Training is achieved by looking for \(\theta\) that maximize
\[
L = \frac{1}{T} \sum_{t}\log f(w_{t},w_{t-1}\cdots,w_{t-n+1}; \theta).
\]
And output layer is a softmax layer,
\[
\hat{P}(w_{t}|w_{1},\cdots,w_{t-1}) = \frac{e^{y_{w_{t}}}}{\sum_{i}e^{y_{i}}}.
\]
2.4 Conclusions
Experiments on two corpora (1) more than one million samples (2) a larger one with above 15 million words. Could yield much better perplexity (a metric to evaluate language models). Since it take advantage of learned distributed representation to fight curse of dimensionarlity, each training sentence informs the model about a combinational number of other sentences.