[Paper reading] Precision and Recall for Time Series.
This paper was proposed by my team leader one month ago, she thought we can apply these new metrics to our current Anomaly Detection project. I read it and think the ideas are very interesting therefore would like to make a note to summarize it.
1. Introduction
For anomaly detection tasks in real world, many of them are under time series scenarios. The anomalies are usually occur over a consecutive sequence of timestamps, in other words, the anomalies are range-based rather than point-based. As you can image, it will looks like this:
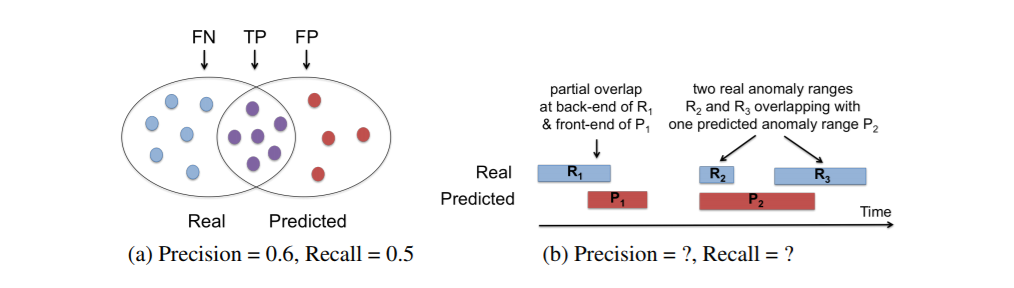
Therefore if the precision and recall are still calculated based on point-based, the real model performance might be misrepresented. The author of the paper proposed a new customized model which can be used to evaluate and compare the anomaly detection algorithms in time series scenarios. Also, outside the scope of model evaluation, this new model can be used as the objection function for ML algorithms’ training.
2. Problem Motivation and Design Goals
In point-based case, a predicted anomaly is either a TP (True Positive) or an FP (False Positive). In range-based case, it will take the range as the basic unit: a predicted anomaly range might partially overlap with real anomaly ranges, therefore it will be partially a TP or partially an FP at some time. As figure shows above, the overlap is important.
New model has following design goals:
- Expressive: could capture overlap position and cardinality
- Flexible: support adjustable weights across multiple criteria for domain-specific needs
- Extensible: support inclusion of additional domain-specific criteria that don’t have prior knowledge
Here the cardinality means: specific domain might care if each independent anomaly range is detected as a single unit or not. For example, when a real anomaly range is captured, the case that it overlap with multiple predicted anomaly range might be worse than overlap with a single predicted anomaly range.
So compared with range-based, point-based only count the overlap size.
3. Precision and Recall for Ranges
Suppose there is a set of real anomaly ranges \(R = \{R_{i}\}\) and a set of predicted anomaly ranges \(P = \{P_{j}\}\), \(N\) is the number of data points, \(N_{r}\) is the size of set \(R\) and \(N_{p}\) is the size of set \(P\).
3.1 Range-based Recall
The calculation of \(Recall_{T}(R, P)\) will iterates over the set of anomaly range \(R\), then average over the number of real anomaly ranges,
\[
Recall_{T}(R, P) = \frac{1}{N_{r}} \sum^{N_{r}}_{i=1} Recall_{T}(R_{i}, P).
\]
Then for \(Recall_{T}(R_{i}, P)\) the follow components are considered:
- Existence: catching the existence of an anomaly
- Size: size of correctly predicted portion of \(R_{i}\)
- Position: relative position of correctly predicted portion of \(R_{i}\)
- Cardinality: detecting \(R_{i}\) with single \(P_{j} \in P\) may be more valuable than multiple \(P\)
Capture all of these as a sum of two reward terms weighed by \(\alpha\) and \((1 - \alpha)\),
\[
Recall{T}(R_{i}, P) = \alpha ExistenceReward(R_{i}, P) + (1 - \alpha) OverlapReward(R_{i}, P),
\]
where the overlap reward consists of size reward, position bias and cardinality.
If a anomaly range is identified, i.e. \(|R_{i}\cap P_{j}|\geq 1\) across all \(P_{j}\in P\), then the existence reward will be satisfied, basically it is
\[
ExistenceReward(R_{i}, P) = \left\{
\begin{aligned}
1,& \text{ if } \sum^{N_{p}}_{i=1}|R_{i}\cap P_{j}|\geq 1 \\
0,& \text{ otherwise}
\end{aligned}
\right.
\]
And the overlap reward is consists of size, positive and cardinality. The paper gives the definitions,

the cardinality term serves as a scaling factor for the rewards earned form overlap size and position bias,
\[
CardinalityFactor(R_{i}, P) = \left\{
\begin{aligned}
&1, \text{ if }R_{i}\text{ overlaps with at most one }P_{j}\in P \\
&\gamma(R_{i}, P), \text{ otherwise}
\end{aligned}
\right.
\]
Here \(\gamma() \leq 1\) which should be determined by specific domain. Then the overlap reward is
\[
OverlapReward(R_{i}, P) = CardinalityFactor(R_{i}, P)\sum^{N_{p}}_{j=1}\omega\left(R_{i}, R_{i}\cap P_{j}, \delta \right).
\]
Here both the weight \(\alpha\) and functions (\(\gamma(), \omega(), \delta()\)) are tuning parameters and could be customized in specific domain problems.
3.2 Range-based Precision
Similar with recall calculation, we have
\[
Precision_{T}(R, P) = \frac{1}{N_{p}} \sum^{N_{p}}_{i=1} Precision_{T}(R, P_{i}).
\]
For precision calculation there is no need for existence reward, since precision by definition emphasizes the prediction quanlity. Therefore,
\[
Precision_{T}(R, P_{i}) = CardinalityFactor(P_{i}, R)\sum^{N_{r}}_{j=1}\omega\left(P_{i}, P_{i}\cap R_{j}, \delta \right).
\]
4. Experiments Study and Conclusions
Next the authors ran a bunch of experiments with diverse datasets and anomaly detection algorithms, some results are listed here
- position bias sensitivity is captured by ranged-based recall, which cannot be captured by the point-based recall
- range-based precision is more range-aware than point-based precision and therefore can judge exactness of rang-based predictions more accurately
- range-based model’s expressiveness for recall and precision carries into combined metrics like F1 score
- new model’s flexibility and generality over the NAB scoring model
Overall it illustrated that the new metrics are expressive, flexible and extensible with a number of tunable parameters.