[Paper reading]: Factorization Machines.
1. Introduction
In this paper, a new model class: Factorization Machine is proposed with several advantages -
- Allow parameter estimation (for feature interaction) under huge sparse data (like recommender systems), where SVMs fail to learn reliable hyperplane;
- Can be optimized in primal form (rather than SVM to be solved in dual form) in linear time;
- As a general predictor to work with any real valued features rather than other factorization models (SVD++, PITF, FPMC, etc) that have restrictions on inputs; and actually by using right indicators in the input feature vectors, FM are identical or very similar to many of the specialized models that are only applicable only for specific task.
2. Prediction Under Sparsity
General supervised learning task is learn a mapping or function: \(f: x \in R^{n}\rightarrow y\). Here the problem need to deal with is high sparsity in data, this usually raised in domains with categorical features take high dimensions like ID features. For example, on movie retail website, it records which user \(u\in U\) rates a movie \(i\in I\) with rating \(r\) from 1 to 5, specifically:
\[
\begin{aligned}
& U = \{\text{Alice }(A), \text{Bob }(B), \text{Charlie }(C), \cdots\} \\
& I = \{\text{Titanic }(TI), \text{Notting Hill }(NH), \cdots\}
\end{aligned}
\]
the task is to predict rating.
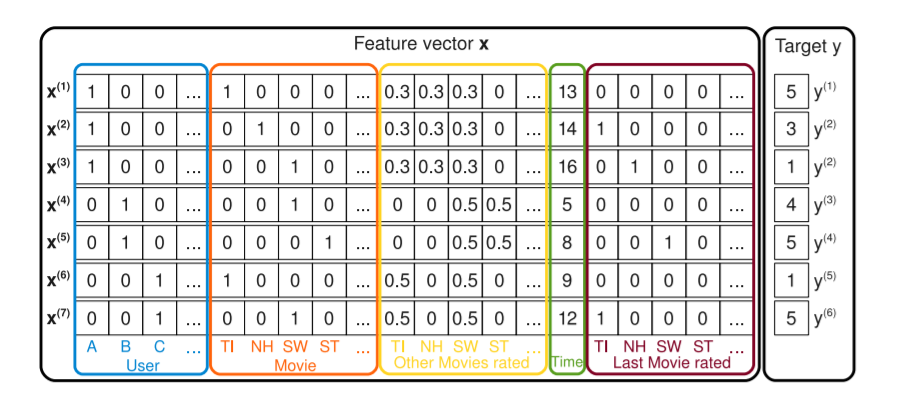
As you can see user ID and movie ID are encoded as one-hot vector and high sparsity is very easy to notice.
2.1 Factorization Machines (FM)
The explicit form of FM is as follows (degree \(d=2\): only consider 2-way feature interactions):
\[
\hat{y}(\mathbf{x}) = w_{0} + \sum^{n}_{i=1}w_{i}x_{i} + \sum^{n}_{i=1}\sum^{n}_{j=i+1}\langle\mathbf{v}_{i}, \mathbf{v}_{j} \rangle x_{i}x_{j},
\]
where \(n\) is the number of input features, the model consists of a bias (constant) term \(w_{0}\), linear weights \(\mathbf{w}\in R^{n}\) (just like linear regression) and interaction weights \(\mathbf{V}\in R^{n\times k}\) and
\[
\langle\mathbf{v}_{i}, \mathbf{v}_{j} \rangle = \sum^{k}_{f=1}v_{if}v_{fj},
\]
is the dot product (inner product) of row \(i\) and row \(j\) of \(\mathbf{V}\). This is key part of FM. For other models like linear regression, if we want to model on 2-way feature interactions, this part would be
\[
\sum^{n}_{i=1}\sum^{n}_{j=i+1}w_{ij}^{(2)}x_{i}x_{j}
\]
where \(w^{(2)}_{ij}\) is the \((i, j)\)th element of \(\mathbf{W}^{(2)}\in R^{n\times n}\). Therefore, FM models feature interactions by factorizing interaction weight matrix: for positive definite matrix \(\mathbf{W}\) there exists a matrix \(\mathbf{V}\) such that \(\mathbf{W} = \mathbf{V}\mathbf{V}^{\top}\), hence for sufficient large \(k\) FM can express any interaction matrix.
2.2 Parameter Estimation Under Sparsity
In sparse settings there is usually not enough data to estimate interactions between variables directly and independently. And Factorization Machines can estimate interactions well because they break the independence of the interaction parameters by factorizing them. This means that data for one interaction helps also to esimate the parameters for related interactions.
For example, the direct estimation for interaction between feature \(I(user = \text{Alice})\) and feature \(I(movie = \text{Star Trek})\) is 0, since Alice never seen Star Trek before. FM will estimate \(\langle\mathbf{v}_{A},\mathbf{v}_{ST} \rangle\),
- Bob and Charlie have similar interaction with Star War, therefore \(\langle\mathbf{v}_{B},\mathbf{v}_{SW} \rangle\) and \(\langle\mathbf{v}_{C},\mathbf{v}_{SW} \rangle\) are similar;
- Alice will have different factor vector \(\mathbf{v}_{A}\) from Charlie \(\mathbf{v}_{C}\) because she has different interactions with factors of Titanic and Star Wars;
- factor vector of Star Trek are likely to be similar to be one of Star Wars because Bob has similar interactions for both movies.
In total, the dot product of factor vector \(\mathbf{v}_{A}\) and \(\mathbf{v}_{ST}\) will be similar to one of Alice and Star Wars
2.3 Computation and Learning
The time complexity to directly compute FM is \(O\left(kn^{2}\right)\), by reformulating this it could be reduced to linear (\(O(kn)\)), only look at the interaction part:
\[
\begin{aligned}
&\sum^{n}_{i=1}\sum^{n}_{j=i+1} \langle \mathbf{v}_{i}, \mathbf{v}_{j} \rangle x_{i}x_{j} \\
=&\frac{1}{2}\sum^{n}_{i=1}\sum^{n}_{j=1} \langle \mathbf{v}_{i}, \mathbf{v}_{j} \rangle x_{i}x_{j} - \frac{1}{2}\sum^{n}_{i=1}\langle \mathbf{v}_{i}, \mathbf{v}_{i} \rangle x_{i}x_{i} \\
=&\frac{1}{2}\left(\sum^{n}_{i=1}\sum^{n}_{j=1}\sum^{k}_{f=1}v_{if}v_{fj}x_{i}x_{j} - \sum^{n}_{i=1}\sum^{k}_{f=1}v_{if}^{2}x_{i}^{2}\right) \\
=& \frac{1}{2}\sum^{k}_{f=1}\left(\left(\sum^{n}_{i=1}v_{if}x_{i}\right)\left(\sum^{n}_{j=1}v_{jf}x_{j}\right) - \sum^{n}_{i=1}v_{if}^{2}x_{i}^{2}\right) \\
=&\frac{1}{2}\sum^{k}_{f=1}\left(\left(\sum^{n}_{i=1}v_{if}x_{i}\right)^{2} - \sum^{n}_{i=1}v_{if}^{2}x_{i}^{2}\right).
\end{aligned}
\]
And the gradient of FM is:
\[
\frac{\partial \hat{y}(\mathbf{x})}{\partial \theta} =
\left\{
\begin{aligned}
&1,&\text{if }\theta\text{ is }w_{0} \\
& x_{i},&\text{if }\theta\text{ is }w_{i} \\
& x_{i}\sum^{n}_{j=1}v_{jf}x_{j} - v_{if}x_{i}^{2}, &\text{if }\theta\text{ is }v_{if}
\end{aligned}\right.~.
\]
3. Compared with SVM
The explicit form of SVM is as follows:
\[
\hat{y}(\mathbf{x}) = \langle \phi(\mathbf{x}), \mathbf{w} \rangle,
\]
where \(\phi(\cdot)\) is a mapping from raw feature space \(R^{n}\) into a more complex space \(\mathcal{F}\), it is related to the kernel with
\[
K: R^{n}\times R^{n}\rightarrow R, ~K(\mathbf{x}, \mathbf{z}) = \langle\phi(\mathbf{x}),\phi(\mathbf{z}) \rangle.
\]
When using linear kernel: \(K(\mathbf{x}, \mathbf{z}) = 1 + \langle \mathbf{x}, \mathbf{z} \rangle\), and SVM is rewritten as:
\[
\hat{y}(\mathbf{x}) = w_{0} + \sum^{n}_{i=1}w_{i}x_{i},
\]
and it’s obvious that a linear SVM is equivalent to a FM with \(d=1\).
When using polynomial kernel: \(K(\mathbf{x}, \mathbf{z}) = (1 + \langle \mathbf{x}, \mathbf{z} \rangle)^{d}\), suppose \(d=2\), SVM is rewritten as:
\[
\hat{y}(\mathbf{x}) = w_{0} + \sqrt{2}\sum^{n}_{i=1}w_{i}x_{i} + \sum^{n}_{i=1}w_{ii}^{(2)}x_{ii}^{2} + \sqrt{2}\sum^{n}_{i=1}\sum^{n}_{j=i+1}w_{ij}^{(2)}x_{i}x_{j}.
\]
The main difference between SVM and FM is the parametrization: all interaction parameters \(w_{ij}\) of SVM are completely independent; in contrast, FM factorizes interaction parameters, thus \(\langle\mathbf{v}_{i},\mathbf{v}_{j} \rangle\) and \(\langle\mathbf{v}_{i}, \mathbf{v}_{l} \rangle\) depend on each other as they overlap and share parameters (\(\mathbf{v}_{i}\)).
In summary:
- The dense parametrization of SVM requires direction observations for the interactions, which is often missing in sparse setting like recommender systems; parameters of FM can be estimated well even under huge sparsity;
- FM can be directly learned in the primal; non-linear kernel SVM are usually learned in the dual;
- Model form of FM is independent of training data; predictions with SVM depends on data (support vectors);
- FM is still linear model, while SVM may not.
4. Compared with other Factorization Models
4.1 Matrix Factorization
Matrix Factorization (MF) factorizes a relationship between two categorical features (e.g. users and items). The standard input feature \(\mathbf{x}\) is usually binary indicators for each category. A FM using this input is identical to the matrix factorization because \(x_{j}\) is only non-zero for \(u\) and \(i\),
\[
\hat{y}(\mathbf{x}) = w_{0} + w_{u} + w_{i} + \langle \mathbf{v}_{u}, \mathbf{v}_{i} \rangle.
\]
This is the form of matrix factorization model with bias of user and item added.
4.2 SVD++
Koren et al improve the matrix factorization model to SVD++ model for rating prediction in recommender systems. A FM can mimic this by using following input:
\[
x_{j} = \left\{
\begin{aligned}
& 1,&\text{if } (j = i) \text{ and } (j = u) \\
& 1 / \sqrt{|N(u)|},&\text{if }j\in N(u) \\
& 0,&\text{else}
\end{aligned}\right.
\]
where \(N(u)\) is the set of other movies the user has rated. A FM with \(d=2\) could behave as:
\[
\begin{aligned}
\hat{y}(\mathbf{x}) =~& w_{0} + w_{u} + w_{i} + \langle\mathbf{v}_{u},\mathbf{v}_{i} \rangle + \frac{1}{\sqrt{|N(u)|}}\sum_{l\in N(u)}\langle\mathbf{v}_{i},\mathbf{v}_{l} \rangle \\
+~&\frac{1}{\sqrt{|N(u)|}}\sum_{l\in N(u)}\left(w_{l} + \langle\mathbf{v}_{u},\mathbf{v}_{l} \rangle + \frac{1}{|N(u)|}\sum_{l’\in N(u), l’>l}\langle\mathbf{v}_{l},\mathbf{v}_{l’} \rangle\right)
\end{aligned}
\]
here the first line of the equation is the SVD++ model, but FM also contains some additional interactions between users and items in \(N(u)\).
In summary:
- Standard factorization models are not general prediction model like FM, instead they require that the feature vector is partitioned in parts and in each part exactly one element is 1 or 0;
- FM can mimic many factorization models just by feature extractions which makes FM easily applicable in practice.